美國著名文豪馬克‧吐溫留下一段經典名句：「謊言有三種：謊言、該死的謊言與統計數字 (There are three kinds of lies: lies, damned lies, and statistics.）。」目的在於諷刺那些使用統計數據支持卻毫無說服力的報告，以及貶低反對立場的統計結論。我想要用一個發生在台灣的真實案例來呼應馬克‧吐溫的哲言。
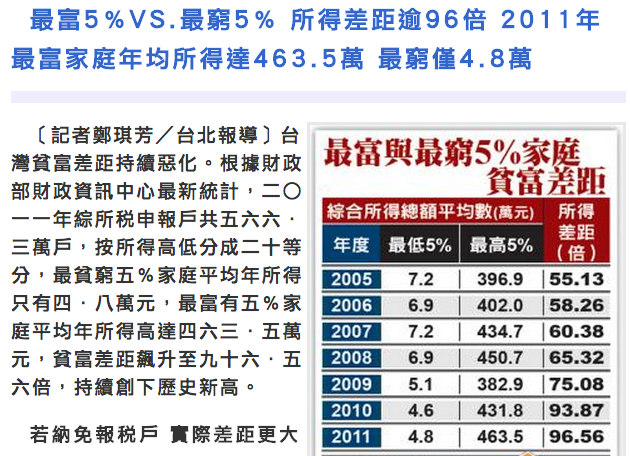
以下是2012年3月27日自由時報的頭條新聞，主要是說明2010年度最窮的5%家庭平均年所得僅4.6萬元，對比最富的5%家庭平均年所得429.4萬元，差距達到93倍，比去年的75倍差距來得更高。
自由時報-貧富差距飆至93倍 歷史新高 http://www.libertytimes.com.tw/2012/new/mar/27/today-t3.htm
再看一則當時經建會主委尹啟銘先生的文章，時間是在上一則新聞過後的兩天 (3/29) 。主要是在闡述國際上常用的是五等分法，即最窮與最富的20%來比較，得貧富差距為6.19倍，相比去年的6.34倍來得低。至於使用最窮與最富的5%來衡量貧富差距（二十等分法）在國際上缺乏理論的根據和無公信力作基礎，因此國際上幾乎無人採用。
尹啟銘-讓國人正確了解當前貧富差距, http://www.ndc.gov.tw/m1.aspx?sNo=0016735
事實上，這種爭論每年都會登上新聞版面，譬如自由時報2013/06/10的頭版新聞
自由時報-最富5％VS.最窮5％ 所得差距逾96倍 http://www.libertytimes.com.tw/2013/new/jun/10/today-t2.htm
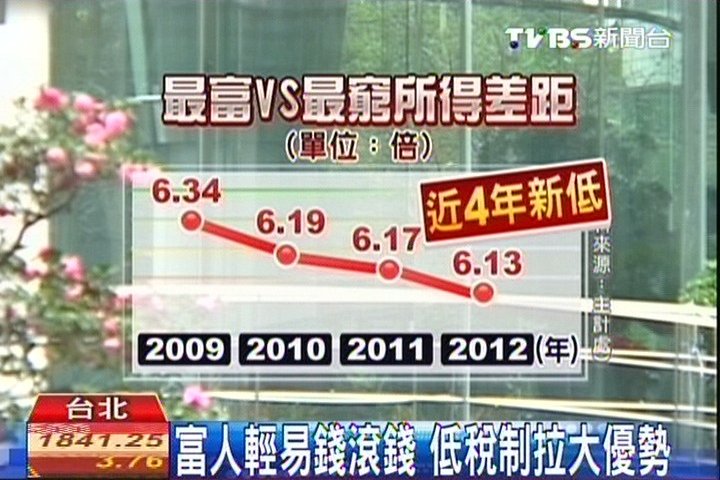
再如TVBS在2014/01/09的影音版新聞
貧富差距擴大？ 逾9成民眾：嚴重！http://news.tvbs.com.tw/entry/517145
平平都是相同來源的每戶年平均所得資料，究竟怎麼一回事？如何從這種裡用統計指標 (statistical index) 各說各話的情勢中明辨是非，是我所關心的問題。從我整理自上述新聞以及官方公佈的家庭收支調查報告勉強可以看出一點端倪。
年度(萬元) 94年 95年 96年 97年 98年 99年 100年
最低5% 7.2 6.9 7.2 6.9 5.1 4.6 4.8
最低20% 29.8 30.4 31.2 30.4 28.2 28.9 29.6
最高20% 180 183 187 184 179 187 183
最高5% 397 402 435 451 383 432 464
看得出來嗎？除了2009年 (民國98年) 國際金融危機之外，最低20%與最高20%的家庭收入2005年以來大致上並無太大的改變。但是最低5%在2009年之後明顯的下降，最高5%則有明顯的上升趨勢。
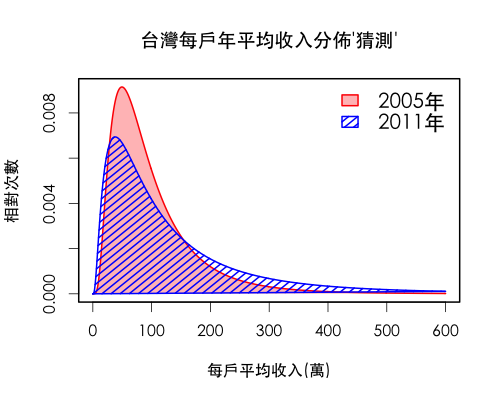
最後，我參考美國每戶收入的直方圖，再根據二十等分位的統計指標來回推台灣在2005與2011年的每戶年平均收入分布圖。先看下圖的右半部 (富人部分)，可以發現藍色 (2011年) 的圖形的右邊拖著一條比紅色 (2005年) 圖形要高的尾巴；再看左半部 (窮人部分)，雖然有一點不明顯，不過還是可以發現藍色比紅色圖形更靠左邊。與其追究政府官員還是新聞報導的統計指標孰是孰非，我以為透過這張分布圖來回答更加明確。這邊用統計人的角度murmur一下，有關單位不要只公布統計指標，Data Open吧。
台灣每戶年平均收入猜測
我寫這篇文章的主要目的，不在於討論台灣社會貧富差距 (這類的討論真的很多，光是用幾等分法來衡量貧富差距就吵不完了)，而是在於呼應馬克‧吐溫的哲言。要知道，同樣的資料集可以產生各種不同的統計指標，每一種統計指標都有獨特的意義以及適用的時機。統計指標並沒有好壞之分，可惡的是因為立場的不同，而使用特定指標來做為宣傳工作的壞蛋。
最低20%與最高20%的家庭收入2005年以來大致上太大的改變。
筆誤??
已修正，感謝提醒！
You did a good job to illustrate thepossibilities of reaching different conclusions with the same data. So. What are the right ways to demonstrate income inequalities?
From 2005 to 2011 the income distribution became more skewed.
So how to relate skew ness to inequality?
As skew ness increases what is the right way to report inequality?
Let us think more deeply?
When skew ness increases inequality widened?
Prof. Wang Jhonson you know more than I do
Dear Prof Wang,
I agree that the trends of skewness plays important role in the income inequalities.
Based on the property of skewness in positive support (say x > 0), I think a simple index to measure income inequalities could be (median – mean)/std_dev.
貧富差距99倍！最窮5％家庭年收4.4萬 (2015-07-01)
http://news.ltn.com.tw/news/focus/paper/894078
您好
完全同意你 政府資訊應該更公開
另外
想請教個問題
http://www.storm.mg/article/62618
風傳媒這篇 提到用五等分法 台灣貧富差距變小
想請教：
假設 用五等分法 台灣貧富差距持續所小或平盤
又假設 用20等分法 貧富差距持續擴大
當這兩件事持續發生時
從統計的角度 我們可以推論出 什麼 關於貧富差距的 有趣的結論嗎？
例如 可以推出 skew ness 增加嗎？
年度(萬元) 94年 95年 96年 97年 98年 99年 100年
最低5% 7.2 6.9 7.2 6.9 5.1 4.6 4.8
最低20% 29.8 30.4 31.2 30.4 28.2 28.9 29.6
最高20% 180 183 187 184 179 187 183
最高5% 397 402 435 451 383 432 464
跟據你整理的這組數字 好像看到相對於台灣的答案
為了解釋方便 假設台灣只有100個家庭
讓我們稱 最有錢的家庭第一名 最窮的第100名
讓我們考慮 第6名到第20名的才富加總
民國94年 他們共有1615萬元
但民國100年卻掉到1340萬元
共少了275萬元
平均一個家庭一個月少了大約1.5萬
而第81名到95名的家庭則平均每月只增加440元台幣
如果我上面的推論沒有太大錯誤
五等分法持續拉近 20等分法持續拉開
背後其中一個主因是 第 6至20名的收入持續大下降
更跳躍地說 財富是往5%那邊集中
不是念經濟 也不是念社會系 更不懂統計
如果有荒謬推論 請見諒
我同意你的推論 (不過1615, 1340萬元怎麼算出來的啊~)
180*20=3600 (94年度 第1名至20名的財富加總）
5*397=1985 （94年度 第一名至第5名的財富加總）
3600-1985=1615 （94年度 第6名至第20名的財富加總）
相似的計算方式運用在100年度
183*20=3660
5*464=2320
3660-2320=1340
希望這樣算沒錯
got it. it’s ok!
您好：
您的問題很有趣，我們在討論貧富差距時，會使用一些統計指標來作為衡量標準。譬如五等分法、20等分法計算第一與最後級距的比值，而你提的skewness也可以視為貧富差距指標 (只是沒什麼人用…)。基本上，您提的前提，skewness可以變大也可以變小喔，光透過5%, 20% 80% 95% 不太能定skewness的改變。不過，你提到一件重要的概念，就是兩個年度所得的比較時，不能只單單看一個
國際慣用指標，要看多個。20等分法算出的結果變大，表示極端貧富差距變大，5等分法算出的結果變小，表示小康跟富裕的家庭差距變小，都有不同的解釋意義。此外，把拿20% – 80% 也是一種貧富指標喔。感謝你的回覆 另外 你所做關於太陽花學的研究很有趣！
不會，感謝關注：）